Mean Width Of The Profile Elements (Rsm, Psm, Wsm)

Mean Width Of The Profile Elements (Rsm, Psm, Wsm) | Surface Roughness Parameters

Surface roughness parameters in JIS B 0601

Peaks and valleys in the height direction

Average amplitude in the height direction

Average characteristics in the height direction

Horizontal direction

Hybrid

Areal material ratio curve and probability density function

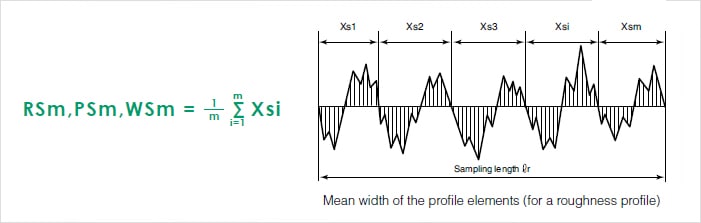
Mean width of the profile elements indicate the average value of the length of the profile element along the sampling length; Xsi is the length of a single profile element. The peaks (valley) that constitute elements have minimum height and length standards such that they will be treated as noise and considered a part of the preceding valley (peak) if the height (depth) is less than 10% of the maximum height or the length is less than 1% of the segment length.

Surface Roughness Parameters

This section explains the main parameters of ISO 4287:1997. Each parameter is classified according to primary profile (P), roughness profile (R), and waviness profile (W) in order to evaluate different aspects of the profile. (When the wavelengths of the waviness and primary profile components are compared, the surface roughness component is the asperity component of that which has the comparatively shorter wavelength.)

Search from the parameters list

Peaks and valleys in the height direction	Arithmetical mean height (Ra, Pa, Wa)
	Maximum height of profile (Rz, Pz, Wz)
	Maximum profile peak height (Rp, Pp, Wp)
	Maximum profile valley depth (Rv, Pv, Wv)
	Mean height of profile elements (Rc, Pc, Wc)
	Total height of profile (Rt, Pt, Wt)
Average amplitude in the height direction	Root mean square deviation (Rq, Pq, Wq)
Average characteristics in the height direction	Skewness (Rsk, Psk, Wsk)
Average characteristics in the height direction	Kurtosis (Rku, Pku, Wku)
Horizontal direction	Mean width of the profile elements (RSm, PSm, WSm)
Hybrid	Root mean square slope (RΔq, PΔq, WΔq)
Areal material ratio curve and probability density function	Load length ratio (Rmr (c), Pmr (c), Wmr (c))
	Profile cut level difference (Rδc, Pδc, Wδc)
	Relative load length ratio (Rmr, Pmr, Wmr)
	Material ratio curve (BAC)
	Probability density function (ADF)

"What is line roughness?" page list