Principles and features of electromagnetic flow meters
Various types of flow meters and flow sensors are available. This section summarizes the principles and features of electromagnetic flow meters.
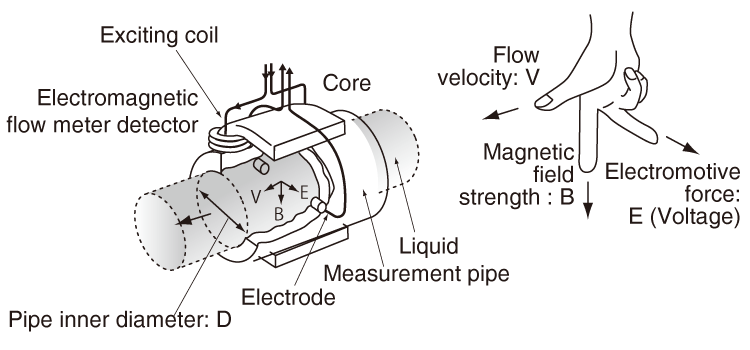
Electromagnetic flow meters detect flow by using Faraday's Law of induction.
Inside an electromagnetic flow meter, there is an electromagnetic coil that generates a magnetic field, and electrodes that capture electromotive force(voltage). Due to this, although it may appear as if there is nothing inside the flow pipe of an electromagnetic flow meter, flow can be measured.
Under Faraday's law of induction, moving conductive liquids inside of a magnetic field generates an electromotive force (voltage) in which the pipe inner diameter, magnetic field strength, and average flow velocity are all proportional. In other words, the flow velocity of liquid moving in a magnetic field is converted into electricity. (E is proportional to V × B × D)
As the flow changes, the electromotive force (voltage) captured by the electrodes changes as follows.
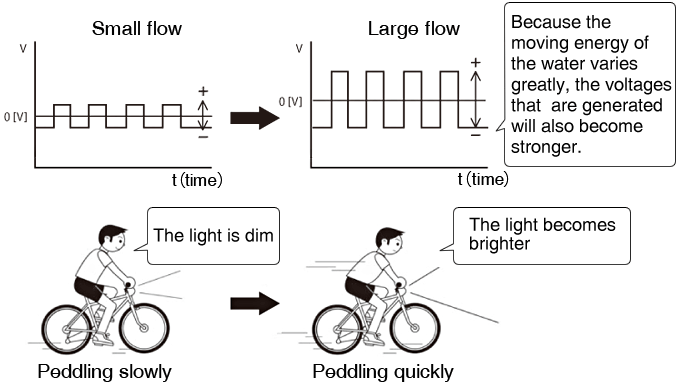
Within the context of the principles listed above, electromagnetic flow meters generally have the following features.
| PROS | ・Unaffected by the temperature, pressure, density,or viscosity of the liquid. ・Able to detect liquids that include contaminants (solids, air bubbles) ・There is no pressure loss. ・No moving parts (improves reliability) |
|---|---|
| CONS | ・Cannot detect gases and liquids without electrical conductivity. ・A short section of straight pipe is required. |
There is one important point when using electromagnetic flow meters. Because electromagnetic flow meters are based on the laws of electromagnetic induction, conductive liquids are the only liquids for which flow can be detected. Whether it is a conductive liquid or not is determined by the presence of electrical conductivity. So, just what is electrical conductivity?
Electrical conductivity generally is a value that expresses the ease for electricity to flow. The opposite numerical value is resistivity, which expresses the level of difficulty for electricity to flow. For units, S/cm (siemens per centimeter) is primarily used. To determine how easily electricity will flow, 1 cm² electrodes are placed 1 cm apart. Using tap water at 100 to 200 μS/cm, mineral water at 500 μS/cm or more, and pure water at 0.1 μS/cm or less as samples, we can provide examples of actual measured electrical conductivity.
In order to calculate electrical conductivity, it is necessary that conditions, such as electrode area and the distance between electrodes, are properly calculated. Because of this, it is fairly difficult to calculate. As a general way to confirm electrical conductivity, an electrical conductivity meter (US$50-1000) can be used to perform this measurement.
H2O itself is a stable molecule, and will not conduct electricity. So, why does electricity flow in water? The secret is that the absence or presence of impurities in the water determine its ability to conduct electricity.
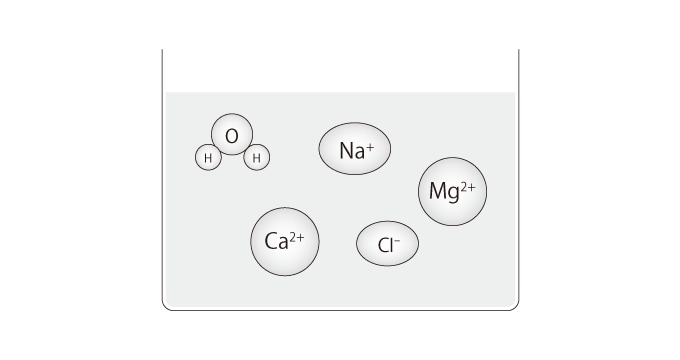
Besides H2O (water molecules), Ca2+ (Calcium ions) and Mg2+ (Magnesium ions) exist within water. The terms hard water and soft water are determined by the amount of ions found within a given amount of water. Because these ions conduct electricity within water, tap water, groundwater and other ion rich waters possess a property that conducts electricity. Also, since pure water is only H2O and does not contain any impurities, it cannot conduct electricity.
When you would simply like to confirm the presence or absence of electrical conductivity, a standard multi-meter can be used. Place the tester in a mode that measures resistance values and place both probes into the liquid. If the needle of the tester moves even slightly towards the zero side, it shows that electricity is flowing.* Conversely, if the needle does not move from ∞ at all, then there is no electrical conductivity. It can be judged that detection with an electromagnetic flow meter is not possilbe.
*As a precautionary measure, confirmation using an electrical conductivity meter is required.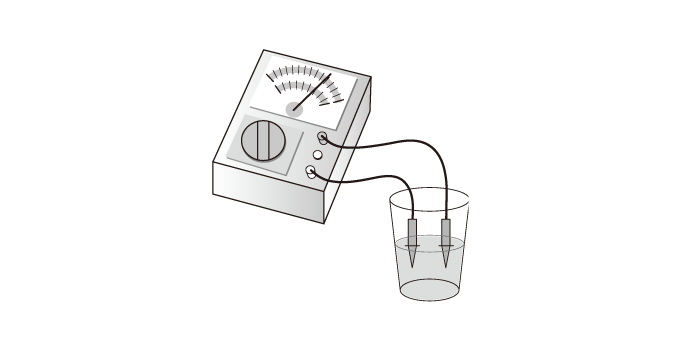
CHAPTER 1
INTRODUCTION TO FLOW METERS
CHAPTER 2
FLOW METER TYPES & PRINCIPLES
