Quiz 2
Q01Effective Color Illumination
Which do you prefer, gold or silver? In terms of value, your answer will always be gold, but color is a personal preference. Due to similar refl ectiveness gold and silver appear almost the same when converted to grayscale.
When using white lighting


Which of the following lighting colors gives the greatest contrast between gold and silver?
- Red
- Blue
- Yellow
- Green
Correct answer:B.Blue
When considering gold and silver colors, silver has a high refl ectivity over a wide range of the visible spectrum while the refl ectivity of gold drops off in the blue wavelength (500 nm) and below. Therefore, when blue lighting is used on a silver/gold target, the gold appears darker.
In the images below, you can see gold appears dark under blue lighting, where as there is little difference when using red lighting (image on the right).
Blue lighting

Red lighting

Blue lighting makes gold appear darker creating the best gold/silver contrast.
Q02Outer Diameter Measurement & Lens Selection
How to go about measuring a 10 mm (0.39") outer diameter on a cylindrical target with machine vision.
Which of the following lenses is generally considered ideal?
- A lens with 6-mm (0.24") focal distance
- A lens with 25-mm (0.98") focal distance
- A telecentric lens
Put (1), (2) and (3) in order of selection priority (most suitable first):
- (2)→(1)→(3)
- (3)→(2)→(1)
- (1)→(2)→(3)
Correct answer:B.(3) → (2) → (1)
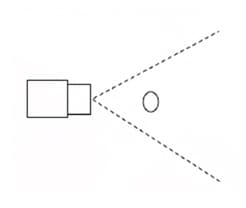
(a) 6-mm (0.24") lens
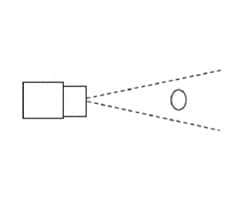
(b) 25-mm (0.98") lens
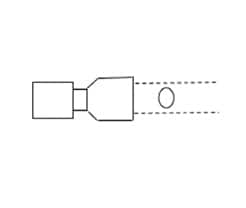
(c) Telecentric lens
When inspecting dimensions using machine vision, lens characteristics can affect the accuracy of an inspection. This question revolves around the differences between three lens types: telecentric, short focal distance and long focal distance. When using a lens that has a short focal distance it typically has a wide angle of view as well. So the size of the captured target will change greatly as the target moves nearer or further from the camera. In other words, when you want to measure dimensions, the variation in measurements will be smaller using a lens with an angle of view closer to 0 degrees. Therefore, when comparing 25-mm (0.98") and 6-mm (0.24") lenses, a 25-mm (0.98") lens with a narrower angle of view is more suitable for the inspection.
A telecentric lens is optically designed so that the angle of view is almost 0 degrees, and is well suited for dimension inspections. Hence a telecentric lens would be the best.
For these reasons, the correct answer isB. (3)Telecentric lens→(2)25-mm (0.98") lens→(1)6-mm (0.24") lens
Q03Pre-processing Image Enhancement Filters
Various pre-processing filters are available for manipulating raw camera images. Effective use of pre-processing filters can dramatically stabilize inspections.
Which filter is the best to give the effect described on the images below?


- (a) Expansion filter, (b) Shrink filter
- (a) Shrink filter, (b) Edge-extraction Y filter
- (a) Shrink filter, (b) Edge-extraction X filter
Correct answer:B.(a) Shrink filter, (b) Edge-extraction Y filter
(a) Using a shrink fi lter will emphasize the black spot. A shrink fi lter reduces the brighter areas of an image, resulting in an expanded black spot.
Raw image

Image with shrink filter

As the white area around the black spot contracts, the black spot expands.
Image with expansion filter

As the white area around the black spot expands, the black spot contracts or disappears.
(b) Using an edge-extraction Y-fi lter, can hide vertical lines. The fi lter emphasizes rows of horizontal contrast in the image, thus removing the vertical lines in an image.
Raw image

Edge-extraction Y-filter

The horizontal direction is emphasized, and vertical lines disappear.
Edge-extraction X-filter

The vertical direction is emphasized, and the contrast of vertical lines is enhanced.
Q04Line Speed and Shutter Speed
In general, to prevent a high speed moving target from being out of focus when capturing images, a fast shutter speed is required. On the other hand, if you are capturing the image of stars in a dark night sky, a longer exposure time is required and a slow shutter speed is needed.
For this example, the image sensor has a field of view of 100mm (3.94") and the CCD size is 500 × 500 pixels*. The target will pass the image sensor at a speed of 1000 mm/second.
Which of the following shutter speeds would be best in order to keep the image (in the above example) in focus under the optimum lighting conditions?
*For ease of calculation, the CCD size has been made 500 pixels × 500 pixels, however in reality this CCD size does not exist.
- 1/500 second
- 1/1000 second
- 1/10000 second
- 1/50000 second

Correct answer:C.1/10000 second
The information outlined here can also be utilized in the manual operation of a digital single-lens reflex camera, so please ensure you know and understand the information thoroughly.
In order to keep an image in focus, it is best to use a fast shutter speed. However, if the shutter speed is too fast, the image may end up too dark as there is not enough exposure. In order to obtain an optimum image capture without losing focus, set the shutter speed using the time it takes for the target to move 1/2 of a pixel as a reference. This is in order to complete exposure in half the time it takes to move the distance of 1 pixel.
- First, find the size of 1/2 a pixel.Field of view is 100 mm(CCD size: 500 pixels ×500 pixels)
100 mm ÷ 500 pixels ÷ 2 = 0.1 mm - Next, find the time it takes to move 0.1 mm.
0.1 mm ÷ 1000 mm/second = 0.0001 seconds = 1/10000 second
Therefore, the answer is 1/10000 second.




![A Technical History of Image Processing Vol.1 [Camera]](/img/asset/AS_46814_L.jpg)
![The Latest Image Processing Applications [Transportation Industry]](/img/asset/AS_71759_L.jpg)

![The Latest Machine Vision Inspections [Food and Medical Industries]](/img/asset/AS_72814_L.jpg)








