Data Acquisition (DAQ)

What is Strain?

Strain is the measurement of the deformation of a particular material relative to its original shape without necessarily specifying the forces that caused the deformation. As such, it represents the displacement between particles within a material and is completely without dimensions since it represents the ratio of lengths.

This section introduces Poisson’s ratio and stress to explain “strain” in terms of strain measurement.

What is Strain?

The topic of “strain” (ε) always comes up when considering the strength and structure of a product.

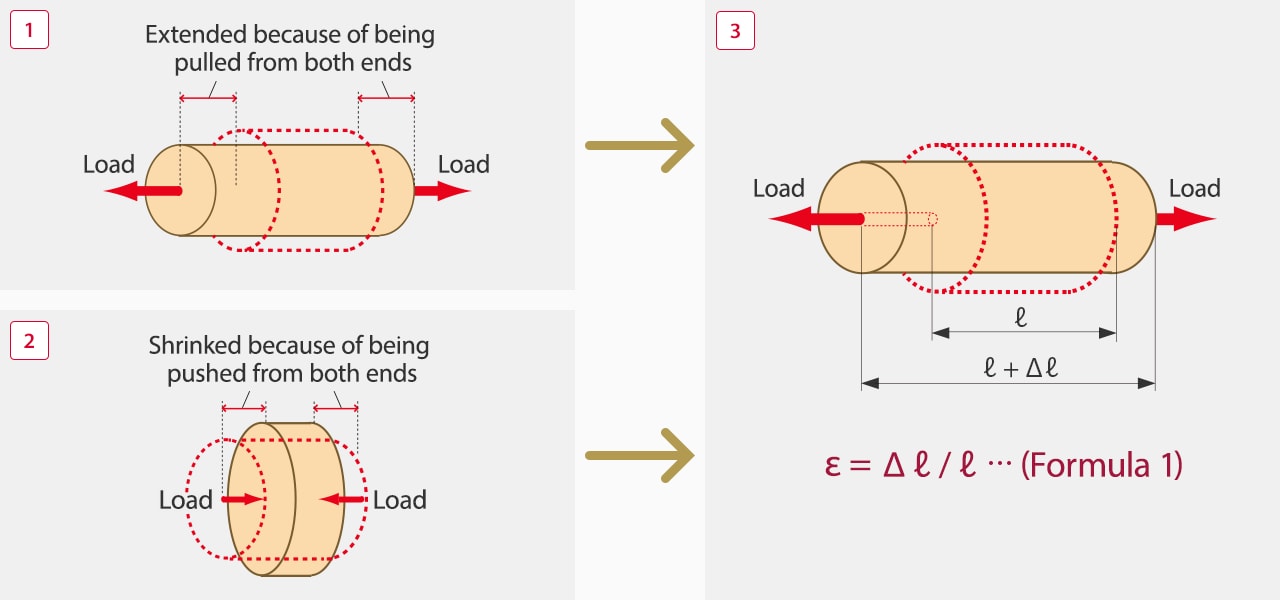
1

For example, if a metallic bar is pulled from both ends, the length will be extended slightly from the original length.
2

Likewise, if a metallic bar is pushed from both ends, the length will be shortened slightly from the original length.
3

Strain (ε) refers to a ratio of expansion/contraction from the original length and is expressed with formula 1.

ε = Δℓ / ℓ …(Formula 1)

Unit of Strain

There is no unit for strain because it represents an expansion (contraction) as a ratio. In other words, it is treated as a “unitless” number. However, to indicate that “a given number represents a strain,” “ST” (an abbreviation of strain) or “ε” (because strain is generally represented by the Greek letter ε) is appended after the number. (This is the same way of thinking that is used with “%” and “ppm.”)Because strain represents a small value, micro strain is expressed with the prefix “µ” (micro, 1 × 10⁻⁶) as in “µST” or “µε.”

Ask KEYENCE

Poisson’s Ratio and Stress

If you pull a bar, its diameter will decrease as the bar expands. Strain in the direction of expansion (contraction) is called “longitudinal strain” while the change in the diameter direction (the direction perpendicular to the external force) is called “lateral strain” (εh).

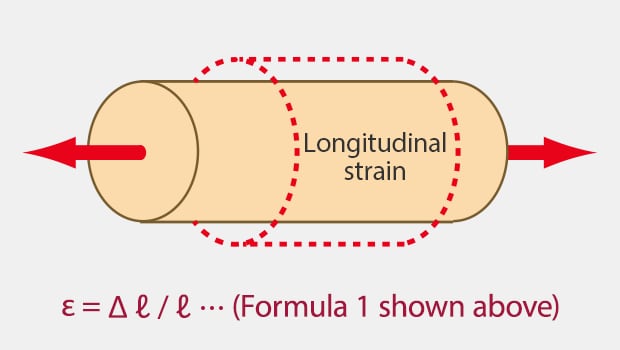
ε = Δℓ / ℓ …(Formula 1 shown above)

Longitudinal strain is a ratio in the direction of expansion (contraction) of an object.

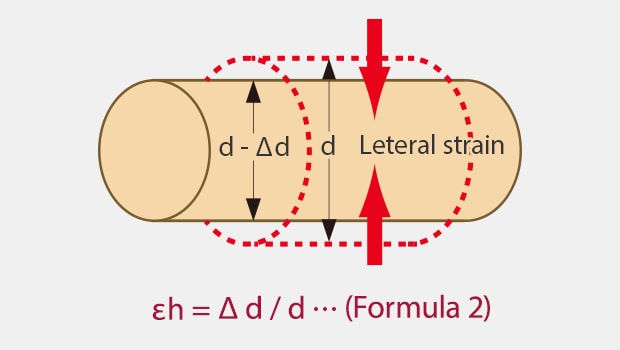
εh = Δd / d …(Formula 2)

Lateral strain is a ratio of the change in the diameter direction.

The ratio between longitudinal and lateral strains is called the “Poisson’s ratio,” and general metallic materials have a ratio around 0.3.
ν = ｜εh/ε｜ — Formula 3

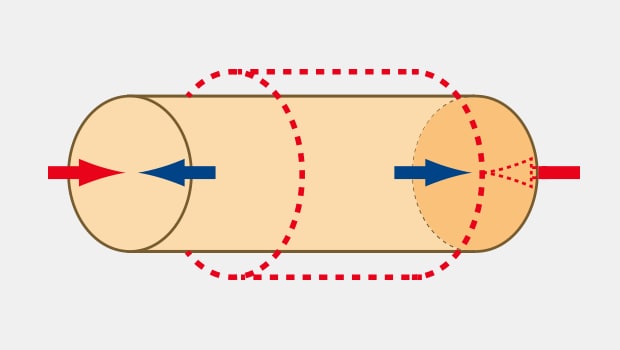
Then, what force is working in the bar being pulled? In the bar being pulled, a force to return to the original shape is working (the magnitude is the same as that of the pulling force). Due to this working force, the bar will return to the original shape if you stop pulling it.

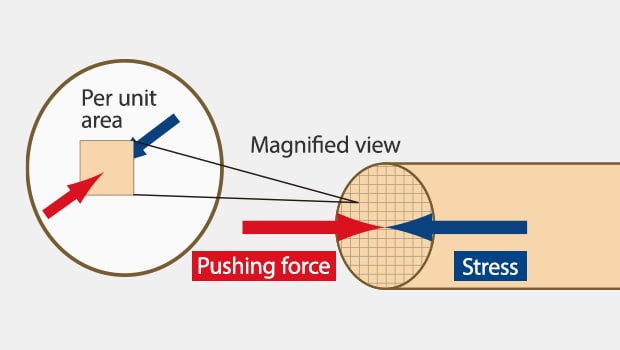
The value obtained by dividing this repelling force by the cross-sectional area (the value converted to per unit area) is called “stress” (σ). With the external pulling force as P (N) and the cross-sectional area as a (m²), the stress is obtained as follows.

σ = P / a — Formula 4

Does Strain Have a Direction (Sign)?

Strain also has a direction and the plus or minus sign is attached to express the direction of expansion or contraction.
Pulling (expansion): plus, contraction: minus

Price

Relationship Between Stress and Strain

The relationship between stress and strain has been obtained experimentally.

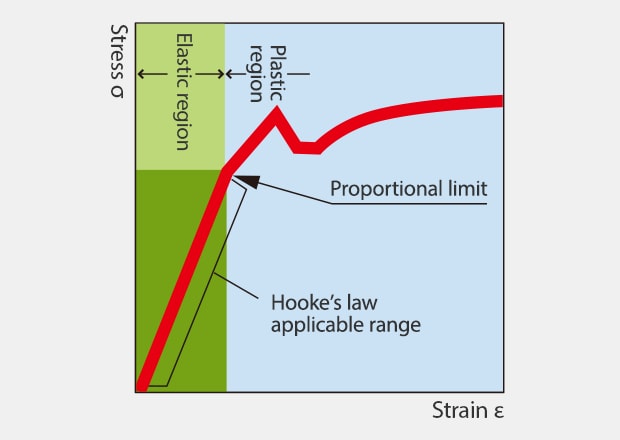
Let’s take a metallic bar as an example. If it is bent only slightly, the bar will return to the original straight state. However, if the bar is bent forcefully, it will not return to the original state but will remain bent. The amount of bending (strain amount) that allows for a return to the original state is called the “elastic region” and the region above it is called the “plastic region.” In the elastic region, there is a linear relationship between stress and strain, which is known as “Young’s modulus” or the “modulus of longitudinal elasticity” and is generally expressed as “E.”
Once Young’s modulus (the modulus of longitudinal elasticity) is known, you can calculate the stress from the strain amount.

σ = (material-based constant E) × ε — Formula 5

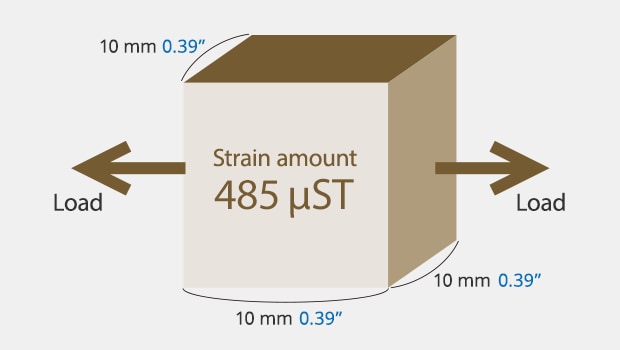
Let’s Obtain the Stress (the Applied Force) From the Strain Amount

Let’s obtain the stress by assuming that a strain of 485 µST has been measured after pulling the steel bar in the figure.

SS400
(Rolled steel for general structures)
Dimensions: 10 mm 0.39″ square bar

Conditions: Young’s modulus (the modulus of longitudinal elasticity) of SS400 E = 206 GPa, 1 Pa = 1 N/m²
From formula 5:
σ = E × ε = 206 GPa × 485 µST
= (206 × 10⁹) × (485 × 10⁻⁶) = 99.9 MPa
From formula 4:
P = σ × a = 99.9 MPa × (0.01 m × 0.01 m)
= (99.9 × 10⁶) × (1 × 10⁻⁴) = 9.99 kN
= Approximately 10 tons
Hence, it is assumed that the bar has been pulled with a load of approximately 10 tons.

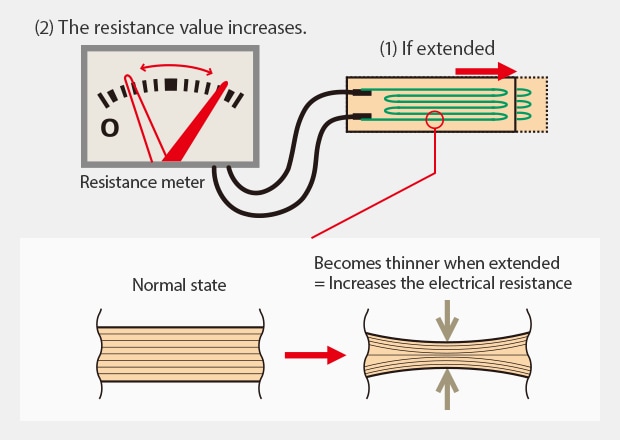
A strain gauge is an extremely thin metallic wire. If it is pulled, the gauge will become even thinner, which will make it more difficult for electricity to flow, thereby increasing the resistance.

Strain Gauges

Strain gauges use the principle that the resistance of a metal changes with its expansion/contraction.

With the original resistance as R (σ), the change in the resistance as ΔR (σ), and the strain amount as ε, this principle is expressed as follows.

ΔR / R = constant of proportionality K × ε — Formula 6

The constant of proportionality K is called the “gauge factor,” which has been determined on the basis of the metal (alloy) used for the strain gauge. With no load, the resistance of a strain gauge is generally 120 σ. During general strain measurement, the change in the resistance is several σ at most, so you need to take specific measures to achieve accurate strain measurement.

Unit of Strain

Let’s obtain the stress (the applied force) from the strain amount. Here, it is assumed that the strain amount is 485 µST, the resistance of the strain gauge is 120 σ, and the gauge factor is 2.00. From formula 6:
ΔR = 2.00 × 485 µST × 120 σ = 0.1164 σ
Surprisingly, the resistance has changed only by 0.1164 σ. The change is as subtle as this.

How to Calculate Strain of a Material

The strain of a material is defined as the change in length over the original length. For example, if a meal rod originally measures 100 cm and stretches to 101 cm under load, the strain would be calculated as the new length minus the original length over the original length. In this case, that is:

ϵ= (101 – 100)/100 => ϵ=1/100 => ϵ=0.01

Alternatively, if you’re looking for a quick way to calculate strain for strain measurement applications, we suggest investing in a KEYENCE data logger or multi-input data logger, such as the NR-X Series or the NR-500 data logger, and a strain gauge.

View Catalog

What are the Different Types of Strains

It’s important to note that there are different types of strains, and all refer to the change in the ratio between the original measurement and the change in length. These include:

Tensile Strain: Occurs when a material elongates. It's a measure of the stretching of the material.
Compressive Strain: Occurs when a material is compressed or shortened.
Shear Strain: Occurs when the material is subjected to forces in opposite directions, causing it to shear or slide. This type of strain is characterized by a change in the shape of the material without a volume change.

Ask KEYENCE

What is the Difference Between Stress and Strain

Stress and strain are different but related contexts in material science. Stress is the force applied per unit area within materials leading to deformation. It’s usually measured as pressure. Strain, on the other hand, is the deformation or displacement of material that results from applied stress. Since it represents a ratio of lengths, it’s a dimensionless measurement.

Experience Demo / Test

What is the Importance of Strain in Materials?

Strain is a crucial measurement in material science and engineering, as it helps understand how materials deform under various loads, which helps predict their behavior in real-world applications.

This measurement is used to ensure the structure can withstand expected loads without failing, and it's one of the key parameters in material testing, as it helps determine material properties, such as elasticity, ductility, and ultimate tensile strength of a particular material.

Price

Different Causes of Strain in Materials?

The application of mechanical forces, such as tensile, compressive, and shear forces, mainly causes strain. Another factor is temperature fluctuation, which causes materials to expand or contract due to heating or cooling, inducing strain. Environmental factors, such as corrosion, moisture absorption, and other factors, may cause certain materials to shrink, swell, or deform, which leads to strain.

Another reason strain might occur within the material is the residual stress introduced by various manufacturing processes like welding, casing, and machining. These can lead to stress even without external force or load.

Need more solutions for calculating strain? Visit our website today!

Ask KEYENCE